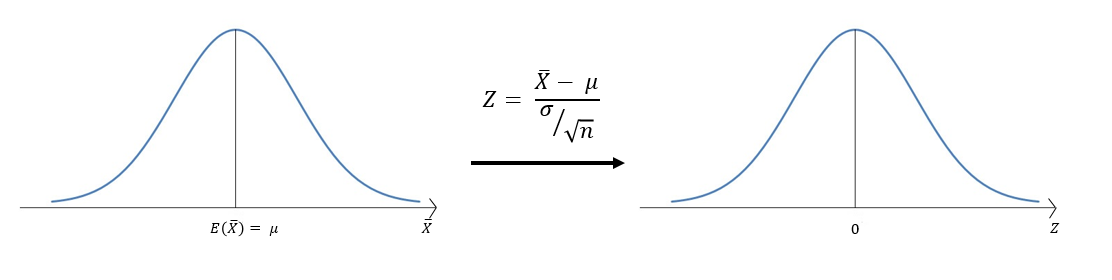블로그

 이번에는 t분포에 대해 정리하려고 한다.

 t분포는 연속확률분포의 하나로써, 정규분포인 모집단의 평균을 추정해야 하지만 표본의 크기가 작고 모집단의 분산을 알 수 없는 경우에 이용된다고 한다.

 t분포는 Student's t-distribution이라고 불리기도 하는데, 그 이유는 처음 t분포를 발견한 William Sealy Gosset이 논문을 발표할 때 Student라는 가명을 사용했기 때문이다. 왜 그랬냐하면 그가 다니던 맥주회사 기네스에서 그가 본명으로 발표하는 것을 원치 않았는데, 자신들이 t분포를 사용한다는 것을 경쟁사한테 알리고 싶지 않았던 것이다.

1. 정의

 $Z$는 표준정규분표 $\mathcal{N}(0, 1)$를 따르는 확률변수, $Q$는 자유도 $k$인 카이제곱분포를 따르는 확률변수이고 둘이 독립일 때, 다음과 같이 정의되는 확률변수 $T$는 자유도가 $k$인 t분포를 따른다. 왜 이렇게 정의되었는지는 차차 생각해보기로 하자.

$$T = \frac{Z}{\sqrt{\frac{Q}{k}}} \Rightarrow T \sim t_k$$

 그리고 이 확률변수는 아래와 같은 확률밀도함수를 갖는다.

$$f(t) = \frac{\Gamma[\frac{(k+1)}{2}]}{\sqrt{\pi k} \Gamma(\frac{k}{2})}\cdot\frac{1}{[\frac{t^2}{k} + 1]^{\frac{(k+1)}{2}}}, \quad -\infty < t < \infty$$

 증명은 가볍게 넘어가고(^^), 확률밀도함수의 그래프가 어떻게 생겼는지 보자.

2. 그래프

 왼쪽 위의 그림부터 보면, 파란색이 정규분포곡선($\mathcal{N}(0, 1)$)을 나타낸 것이고 빨간색이 자유도가 1인 t분포의 곡선을 나타낸 것이다. 두 곡선의 모양을 비교해보면 t분포는 정규본포와 비슷하게 종 모양이지만 양쪽 꼬리가 더 두껍고, 봉우리는 더 낮은 것을 볼 수 있다. 그리고 자유도가 커질수록 점점 정규분포와 가까워지며 자유도가 30(맨 오른쪽 아래)인 그림을 보면 거의 똑같아지는 것을 볼 수 있다. 그래서 여기서 자유도를 nomality parameter라고 부르기도 한다. 사실 이 부분에서 자유도가 커지면 왜 정규분포와 가까워지는지, 이게 t분포의 본질과 어떤 관련이 있는지 더 탐구해보고 싶지만.. 요즘 시간이 없어서 타협모드이므로.. 아쉽지만 넘어가기로 한다.

3. 표본분산과의 관계

 처음에 t분포를 모집단이 정규분포이고, 모평균을 추정하고 싶은데 모분산을 알 수 없고 표본의 크기가 작은 경우에 활용할 수 있다고 했다. 상황을 한 번 상상해보자.

• 어떤 모집단이 있고, 이 모집단은 정규분포를 따르는 것 같다.
• 이 모집단의 모평균을 추정하고 싶은데, 모분산을 몰라서 Z 통계량을 이용한 통계적 추정 방법을 없다.
• 게다가 표본의 크기 $n$이 30보다 작아서 중심극한정리에 의해 표본평균의 분포가 정규분포라고 할 수도 없을 것 같다.

 이 상황에서 어쨌든 우리는 표본을 뽑을 수 있고, 보통은 중심극한정리와 Z 통계량을 이용해서 추정을 하였지만, 이번에는 그럴 수 없는 상황이다. 그러면 우리가 알고 있는 것은 뭔가? 우리는 표본분산 $s^2$은 알 수가 있다. 따라서 Z통계량을 아래와 같이 수정해보자.

$$\frac{\bar{X} - \mu}{\frac{\sigma}{\sqrt{n}}} \Rightarrow \frac{\bar{X} - \mu}{\frac{s}{\sqrt{n}}}$$

 단순히 모분산을 알 수가 없으니 표본분산을 이용해서 통계량을 바꿔본 것이다. 그런데 이 바뀐 통계량을 $\sigma$로 나누어주면 다음과 같은 것을 발견할 수 있다.

$$\frac{\frac{\bar{X} - \mu}{\sigma}}{\frac{s}{\sqrt{n}\sigma}} = \frac{\frac{\bar{X} - \mu}{\frac{\sigma}{\sqrt{n}}}}{\sqrt{\frac{s^2}{\sigma^2}}}$$

$$\Rightarrow \frac{\bar{X} - \mu}{\frac{\sigma}{\sqrt{n}}} \sim \mathcal{N}(0, 1), \quad \frac{s^2}{\sigma^2} \sim \frac{\chi_{n-1}^2}{n-1}$$

 즉, 처음에 정의한 t분포를 따르는 확률변수의 모양 $T = \frac{Z}{\sqrt{\frac{Q}{k}}}$와 같은 형태이므로, 통계량 $\frac{\bar{X} - \mu}{\frac{s}{\sqrt{n}}}$는 자유도가 $n-1$인 t분포를 따른다. 이 통계량을 t통계량이라고 하는데, 우리는 이것을 가지고 위와 같은 상황에서 통계적 추정이나 가설검정을 해 볼 수가 있게 된다. 

 통계를 공부하다 보니 굉장히 불편한 것을 하나 만나게 됐다.

 그것은 바로 표본에서 분산을 정의할 때 원래 알던 분산의 정의(편차의 제곱의 평균)가 아닌 다른 방식으로 정의한다는 것이다. 즉, 표본분산은 편차의 제곱을 표본의 크기로 나누는 것이 아니라, (표본이 크기-1)로 나누어 준다.

$$s^2 = \frac{1}{n} \sum_{i=1}^{n}(X_{i}-\bar{X}) \quad (X)$$

$$s^2 = \frac{1}{n-1} \sum_{i=1}^{n}(X_{i}-\bar{X}) \quad (O)$$

 이렇게 정의하게 된 연유를 좀 찾아 보니, 자유도랑도 연관이 있는 것 같고, 여러 가지 설명들이 있더라. 그런데 자유도로 설명하는 것은 아직 내 수준에서는 도저히 이해가 안되고, 그나마 수긍이 되는 설명으로 정리해본다.

 먼저 불편추정량(Unbiased Estimate)이라는 것에 대해서 알아야 한다. 모집단에서 표본을 뽑았을 때 우리는 표본평균이나 표본분산 등의 표본 통계량을 계산할 수 있다. 그런데 표본을 뽑아 통계량을 계산하는 행위 자체의 근본적인 목적이 바로 모집단의 모수를 추정하는 것이다. 이런 모수를 추정하기 위한 표본 통계량들을 추정량(Estimate)이라고 한다.

 아마도 추정량에 대한 개념이 없이 나보고 표본평균이나 표본분산을 계산하라고 했으면 원래 일반적인 평균과 분산의 개념으로 계산을 했을 것이다. 평균은 (모든 원소들의 합/집단의 크기), (분산은 편차의 제곱의 합/집단의 크기) 이런 식으로. 그런데 앞에서 말했듯이 표본을 추출하는 것 자체가 모집단의 모수를 추정하는 것이므로, 통계학에서는 표본 통계량을 '추정량으로써' 간주하여 다르게 정의하는 듯하다. 즉, 추정량의 역할을 해야하므로 기존의 알던 정의와는 다르게 정의될 수 있다는 것을 받아들여야 마음이 편해진다. 

 목적 자체가 모집단의 모수를 추정하는 것이므로, 추정량은 모집단의 모수를 잘 추정할 수 있도록 정의되는 것이 좋다. 좋은 추정량의 조건이 4가지는 아래와 같다.

1) 불편성 (Unbiasedness)

2) 효율성 (Efficiency)

3) 일치성 (Consistency)

4) 충분성 (Sufficiency)

 여기서 표본분산을 계산할 때 $n$이 아니라 $n-1$로 나누어주는 이유와 관련이 있는 것은 1) 불편성이다. 불편성이란, 편향이 없다(Unbiased)라는 뜻이다. 그렇다면 편향이 있다 or 없다 라는 것은 무엇을 의미하는 걸까? 이런 상황을 생각해보자. 모집단의 모수를 파악하기 위해 표본을 뽑아 표본 통계량을 추정량으로 이용하려고 한다. 이 때 표본평균을 이용한다고 해보자. 표본평균은 중심극한정리에 의해 모평균을 평균으로 하는 정규분포를 따른다. 그렇기 때문에 표본을 여러번 뽑아도 표본평균들은 모평균보다 크게만 나오거나 작게만 나오지 않고 크거나 작게 균등하게 나올 것이다. 즉 표본평균은 그 자체로 편향되지 않는 불편성을 지니고 있다. 따라서 우리가 일반적으로 생각하는 평균의 정의가 아래처럼 그대로 적용될 수 있다. 

$$\bar{X} = \frac{1}{n}\sum_{i=1}^n X_{i}$$

 즉, 이것을 통해 불편성이라는 것을 수학적으로 정의하자면, 표본의 추정량의 기댓값이 모수와 같아야 한다고 말할 수 있다(표본평균이 그런 것처럼). 따라서 표본평균은 불편추정량으로써 다음을 만족하는 것이다($\mu$는 모평균).

$$E(\bar{X}) = \mu$$

 하지만 표본분산은 어떨까? 표본분산도 표본평균처럼 모분산을 기준으로 크거나 작거나 균등하게 나올까? 즉 불편추정량의 조건인 다음을 만족할까?

$$E(s^2) = \sigma^2$$

 이것을 확인해보기 위해, 우리가 원래 알고 있던 분산의 정의, '편차제곱의 합의 평균'으로 한 번 확인해보자. 모평균은 $\mu$, 모분산은 $\sigma^2$라고 할 때,

$$\begin{matrix} E(s^2) &=& E(\frac{1}{n}\sum_{i=1}^n (X_{i} - \bar{X})^2) \\ &=& \frac{1}{n}E(\sum_{i=1}^n (X_{i}^2 - 2X_{i}\bar{X} + \bar{X}^2) \\ &=& \frac{1}{n} E(\sum_{i=1}^n X_{i}^2 - 2\bar{X}\sum_{i=1}^n X_{i} + \sum_{i=1}^n \bar{X}^2) \\ &=& \frac{1}{n} E(\sum_{i=1}^n X_{i}^2 - 2n\bar{X}^2 + n\bar{X}^2 ) \\ &=& \frac{1}{n} \sum_{i=1}^n E(X_{i}^2) - E(\bar{X}^2) \\ &=& \frac{1}{n} \sum_{i=1}^n (\mu^2 + \sigma^2) - (\mu^2 + \frac{\sigma^2}{n}) \\ &=& \frac{n-1}{n}\sigma^2 \end{matrix}$$

 계산해보니 $E(s^2) = \sigma^2$를 만족하지 않는다. 즉, 표본분산은 불편성을 만족하는 불편 추정량이 아니다! 다시 말해 표본분산은 '좋은 추정량'이 아니다. 따라서 우리는 표본분산이 좋은 추정량이 되게 하기 위해 정의를 약간 수정해주어야 한다. 그것은 바로 분모 $n$을 $n-1$로 바꾸어주는 것이다. 바꾸고 위 계산과정을 따르면 정확하게 $\sigma^2$이 나온다. 이것이 바로 표본분산을 구할 때 $n$이 아닌 $n-1$로 나누어주는 이유가 되겠다.

 나는 사실 이것이 상당히 불편한데, 표본분산을 정의할 때 우리가 일반적으로 알고 있는 분산의 정의와 충돌하기 때문이다. 뭔가 표본분산을 '좋은 추정량'으로 만들어주기 위해서 억지로 다시 정의해준 느낌?.... 아무튼 그렇다고 한다.

 통계를 공부하다보니 정규분포 말고도 다양한 확률분포들이 나온다. 이 글에서는 카이제곱분포에 대해 간단히 정리해보려고 한다.

1. 정의

 먼저 정의부터 살펴 보면, 카이제곱분포란 다음과 같이 정의되는 확률변수 $Q$가 따르는 확률분포이다.

$$Q = \sum_{i=1}^k Z_{i}^2$$

 $Z$는 표준정규분포를 따르는 확률변수이다. 즉, 표준정규분포를 따르는 $Z^2$을 $k$개 더한 것으로 정의되는 확률변수는 카이제곱분포를 따른다. $Q$가 카이제곱분포를 따른다는 표현은 아래와 같이 한다.

$$Q \sim \chi^2 (k) \quad or \quad Q \sim \chi_{k}^2$$

여기서 $k$는 더해지는 $Z_{i}^2$의 개수인데, 자유도(degree-of-freedom)라고 한다. 자유도의 정확한 의미에 대해서 찾아봤는데 제대로 이해하기가 상당히 어려운 개념인 것 같다. 일단 여기서는 '더해지는 $Z^2$의 개수'라고 이해해도 별 문제는 없으니, 자유도에 대한 심도있는 이해는 잠깐 미루도록 한다. 확률밀도 함수는 아래와 같다.

$$f(x; k) = \begin{cases} \frac{x^{\frac{k}{2}-1} e^{-\frac{x}{2}}}{2^{\frac{k}{2}} \Gamma(\frac{k}{2})}, & x>0 \\ 0, & otherwise \end{cases}$$

 확률밀도함수가 왜 저렇게 유도되는지에 대한 수학적인 내용에는 흥미가 없다. 수학적인 내용보다는, 이러한 확률변수를 왜 정의하게 되었는지, 그리고 이게 왜 중요하고 어떻게 사용되는지에 더 관심이 많다. 그런 내용을 살펴보기 전에 잠깐 그래프에 대한 직관은 짚고 넘어가고 싶다.

 아참, 기댓값과 분산은 구해보면 아래와 같이 나온다고 한다.

$$E(Q) = k$$

$$V(Q) = 2k$$

2. 그래프

 자유도 $k$가 1, 2, 5, 10일 때의 그래프는 아래와 같다.

 그래프에 대한 직관을 얻기 위해 위 그래프를 자유도에 따라 하나씩 살펴보자. 먼저 자유도 $k = 1$인 경우를 생각해보자. 즉, $$Q = Z^2, \quad Q \sim \chi^2 (1)$$

 이 경우 표준정규분포의 확률밀도함수(왼쪽)와 $Q$의 확률밀도함수(오른쪽)은 아래와 같다.

 오른쪽 $Q$의 그래프에서 가장 먼저 보이는 점은, x축이 양수라는 점이다. 이것은 $Q=Z^2$이니까 당연하다. 그리고 표준정규분포는 평균이 0이기 때문에 0 주변의 수가 가장 많이 샘플링될 것이다. 0 주변의 값들은 제곱하면 더 0에 가까워질 것이다. 다시 말해 0 주변의 값들이 많이 샘플링된다는 것은 $Q$의 입장에서 보면 더 극단적으로 0과 가까운 값들이 샘플링된다는 것이다. 따라서 $Q$의 확률밀도함수는 오른쪽 그래프처럼 그려지게 될 것이다. $k=2$인 경우도 보자.

$$Q = Z_{1}^2 + Z_{2}^2, \quad Q \sim \chi^2 (2)$$

$k=1$일 때보다 완만해지고 꼬리가 좀 더 두꺼워 진 것을 볼 수 있다. 이것은 $Z_{1}^2$과 $Z_{2}^2$이 더해지므로써 나타나는 당연한 현상이다($k=1$일 때 $Z_{1}^2$에서만 샘플링되던 어떤 수에 다른 양수가 더해지는 것이니깐). 이어서 $k=5$인 경우도 보자.

$$Q = Z_{1}^2 + Z_{2}^2 + Z_{3}^2 + Z_{4}^2 + Z_{5}^2, \quad Q \sim \chi^2 (5)$$

 더해지는 수가 많아지니까 당연히 봉우리가 오른쪽으로 점점 옮겨져간다. 계속 가면 어떻게 될까? 통상적으로 $k$가 30이 넘으면 대칭성을 갖춘 정규분포와 가까워진다고 한다.

3. 성질

 카이제곱분포의 가장 기본적인 성질에 대해 짚고 넘어간다. 잠깐 정의를 돌이켜보면 표준정규분포를 따르는 확률변수의 제곱의 합인 $Q$는 카이제곱분포를 따른다고 하였다.

$$Q = \sum_{i=1}^n Z_{i}^2  \Rightarrow Q \sim \chi_{n}^2$$

 그러면 카이제곱분포를 따르는 $Q$와 같은 서로 독립인 확률변수들을 더한 확률변수는 어떻게 될까? 다시 말해, 카이제곱분포를 따르는 $Q_{1}, Q_{2}, Q_{3}, \ldots, Q_{p}$의 자유도가 각각 $k_{1}, k_{2}, k_{3}, \ldots k_{p}$라고 했을 때, 아래와 같이 정의된 확률변수 $Y$는 어떤 분포를 따를까?

$$Y = \sum_{i=1}^p Q_{i}$$

 당연하게도, 각 $Q$들이 $Z^2$들의 합이니까, $Q$들의 합도 $Z^2$의 합이 된다. 따라서,

$$Y \sim \chi_{k_{1} + k_{2} + k_{3} + \ldots + k_{p}}^2$$

 이것을 카이제곱분포의 additivity theorem이라고 한다.

4. 표준분산과의 관계

 모집단이 정규분포 $\mathcal{N}(\mu, \sigma^2)$을 따르고 여기서 뽑은 샘플을 $X_{1}, X_{2}, X_{3}, \ldots, X_{n}$이라고 할 때, 표본분산과 관련된 아래와 같은 값이 카이제곱분포를 따른다고 한다.

$$\frac{(n-1)s^2}{\sigma^2} \sim \chi_{n-1}^2$$

 아직까지는 이게 왜 중요한지는 모르겠다. 나중에 알게 될 것이라고 기대한다. 일단은 봐도 딱히 어떤 의미가 있는지 모르겠으니 수학적인 증명만 해놓고 넘어가기로 하자. 증명은 카이제곱분포의 정의부터 시작한다.

$$\begin{matrix} Q &=& \sum_{i=1}^n Z_{i}^2 \\ &=& \sum_{i=1}^n (\frac{X_{i} - \mu}{\sigma})^2\end{matrix}$$

여기서 분모인 $\sigma^2$을 잠깐 떼어 놓고 보면,

$$\begin{matrix} \sum_{i=1}^n (X_{i} - \mu)^2  &=& \sum_{i=1}^n [(X_{i} - \bar{X}) + (\bar{X} - \mu)]^2 \\ &=& \sum_{i=1}^n (X_{i} - \bar{X})^2 + \sum_{i=1}^n (\bar{X} - \mu)^2 + 2(\bar{X} - \mu)\sum_{i=1}^n(X_{i} - \bar{X}) \\ &=& \sum_{i=1}^n(X_{i} - \bar{X})^2 + n(\bar{X} - \mu)^2 \end{matrix}$$

따라서,

$$\begin{matrix} \frac{\sum_{i=1}^n (X_{i} - \mu)^2}{\sigma^2} &=& \frac{\sum_{i=1}^n (X_{i} - \bar{X})^2}{\sigma^2} + \frac{(\bar{X} - \mu)^2}{\frac{\sigma^2}{n}} \\ &=& \frac{(n-1)S^2}{\sigma^2} + \frac{(\bar{X} - \mu)^2}{\frac{\sigma^2}{n}}\end{matrix}$$

여기서 좌항은 카이제곱분포 정의에 의해

$$\frac{\sum_{i=1}^n (X_{i} - \mu)^2}{\sigma^2} \sim \chi_{n}^2$$

이고, 중심극한정리에 의해 $\bar{X} \sim \mathcal{N}(\mu, \frac{\sigma^2}{n})$이다. 따라서, 표준화한 $\frac{(\bar{X} - \mu)^2}{\sigma^2} \sim \chi_{1}^2$. 그러므로, 카이제곱분포의 additivity theorem에 의해,

$$\frac{(n-1)s^2}{\sigma^2} \sim \chi_{n-1}^2$$ 가 성립한다. 

지난 글에서는 가설검정 중에서 1표본 Z검정에 대해서 정리하였다.

즉, 하나의 모집단과 표본에 대한 가설검정만 다루었다.

이번에는 두 모집단과 표본에 대해서 가설검정 하는 내용을 다루려고 한다(2표본 Z검정).

이 글은 훌륭한 유튜브 강의 영상인 손으로만 푸는 통계 내용을 많이 참조하였음을 밝힌다.

이번에는 어떤 두 모집단 A, B가 있다고 하자. 이때 각 모집단의 모분산 $\sigma_{A}^2$와 $\sigma_{B}^2$는 알려져있다고 가정한다.

그런데 누군가가 모집단 A의 평균 $\mu_{A}$와 모집단 B의 평균 $\mu_{B}$가 같다고 하는 의심스러운 주장을 하고 있다. 이런 의심스러운 주장(가설)을 통계적으로 검정해보려고 한다. 다르게 말하면 우리는 $\mu_{A} = \mu_{B}$임을 주장하고 싶다. 그럼 여기서 귀무가설과 대립가설은 어떻게 될까? 아래와 같이 된다.

귀무가설 $\mathcal{H_{0}}$: $\mu_{A} = \mu_{B}$

대립가설 $\mathcal{H_{1}}$: $\mu_{B} \ne \mu_{B}$  

가설 검정의 기본적인 원리는 1표본 Z검정 때와 같다. 모집단 전체를 조사하기 어려우니까 각각 표본을 뽑아 조사하도록 하고, 아래와 같이 표본을 뽑는다. 이번에도 모집단 A와 B의 모분산이 알려져 있고, 표본의 크기 $n_A$와 $n_B$는 30보다 크다고 가정한다.

표본의 크기가 30보다 크므로, 중심극한 정리에 의해, 다음이 성립한다.

$$\bar{X_{A}}\sim\mathcal{N}(\mu_{A}, \frac{\sigma_{A}^2}{n_{A}}),$$ $$\bar{X_{B}}\sim\mathcal{N}(\mu_{B}, \frac{\sigma_{B}^2}{n_{B}})$$

이전에 1표본 Z검정에서는 모집단의 평균이 특정 값인지 아닌지를 따지는 것이어서 $E(\bar{X})$를 특정 값 $\mu'$인 정규분포로 놓고 표준정규분포를 이용해 p-value를 구하고 유의수준 $\alpha$와 비교했다. 근데 여기서는 귀무가설 자체가 어떤 특정 값과 비교하는 것이 아니고, 값을 모르는 두 모집단의 평균이 같다라는 것이기 때문에 이전과 같이 할 수가 없다. 그래서 약간의 기술을 사용하는데, 다음과 같이 변수를 새로 정의한다. $$Y = \bar{X}_{A} - \bar{X}_{B}$$

이렇게 해주는 이유는 어차피 $\mu_{A}$와 $\mu_{B}$를 알 수 없으니, 둘의 차이를 새로운 관점으로 해서 접근해보겠다는 것이다.

그러면 귀무가설은 $$\mu_{A} = \mu_{B}$$ $$\Leftrightarrow E(Y) = \mu_{A} - \mu_{B} = 0$$

이 된다. 그런데 $\bar{X}_{A}$와 $\bar{X}_{B}$가 각각 정규분포를 따르므로, $Y$는 다음과 같은 정규분포를 따른다. $Y$가 아래와 같은 정규분포를 따른다는 것은 수학적 증명이 필요한데, 자세한 증명은 손으로만 푸는 통계 채널을 참고하도록 하고 여기서는 생략한다. $$Y\sim\mathcal{N}(0, \frac{\sigma_{A}^2}{n_{A}} + \frac{\sigma_{B}^2}{n_{B}})$$

모집단 A, B에서 각각 뽑은 표본의 평균을 $\bar{X_{A, 1}}, \bar{X_{B, 1}}$이라고 하면 $Y_{1} = \bar{X}_{A, 1} - \bar{X}_{B, 1}$이다. 즉, 모집단 A, B에서 표본을 하나씩 뽑으면 위 정규분포에서도 $Y$에 대한 표본을 하나 뽑은 것과 같다. 유의수준 $\alpha$를 0.05로 정했다고 하고, 어쨌든 이 상태에서 $Y$의 분포에 대한 평균과 분산을 알고 있으니 표준정규분포를 이용해서 $Y_{1}$에 대한 p-value를 구할 수가 있다. 만약 구한 p-value가 $\alpha$보다 작으면, 즉 표본이 기각역 안에 있으면 귀무가설을 기각하고 대립가설을 채택할 수가 있게 된다.

다시 말해서, 두 모집단 A, B의 평균의 차이가 0이다 라는 귀무가설이 참이라고 했을 때, 표본을 추출해봤더니 뽑힐 확률이 5%미만인 표본이 나왔다면, 귀무가설이 잘못되었다고 볼 수 있는 것이다. 

이번엔 가설 검정에 대해 정리하려고 한다.

정리하려고 여러 자료를 찾아보던 중 엄청나게 설명을 잘 해놓은 유튜브 영상이 있어, 이 영상에 나온 내용 위주로 정리하려고 한다. 정말이지 너무 설명을 깔끔하게 잘 해놔서 존경스럽다. 나도 이렇게 명확하고 깔끔하게 잘 설명할 수 있으면 좋으련만. 영상 주소는 여기. 나처럼 통계를 공부해보려는 사람에게 아주 유용한 강의가 채널에 잔뜩 올라와있다. 강추!!

그럼 가설 검정에 대한 이야기를 시작해보자.

가설 검정이란, 말그대로 어떤 '가설'이 있을 때, 그 가설이 맞는지 틀린지 통계적인 관점에서 '검정'해보는 것이다.

먼저 어떤 상황에서 가설 검정을 하게 되는지를 보면 좀 더 순조롭게 이해가 된다.

상황 X)

어떤 분포를 알 수 없는 모집단이 있을 때, 어떤 사람 A가 와서 이 모집단의 평균값이 $\mu'$라고 밑도 끝도 없는 주장을 해대고 있다. 나는 대충 어림잡아 봐도 $\mu'$은 아닐 것 같아 상당의 의심이 드는데, 이 사람이 사기꾼인지 아닌지 알아보기 위해 통계적인 방법으로 A의 '가설'을 검증해보려고 한다.

여기서 A의 주장을 즉 가설을 '귀무가설(Null hypothesis)'이라고 한다.

그 이름도 어려운 귀무가설은 돌아갈 귀, 없을 무를 써서 무無로 돌아갈 가설을 의미한다. 즉, 터무니 없는 가설이므로 기각될 가설이라는 뜻이다. 기호로는 보통 $\mathcal{H_{0}}$로 표현한다.

아무리 터무니없어 보여도 귀무가설이 참이 확률이 있다. 따라서 귀무가설은 기각될 수도 있고 채택될 수도 있다. 쉽게 말해 통계적으로 검정을 해보았을 때 기각된다 함은 '옳지 않은 가능성이 높다고 판단'한다는 것이고 채택된다는 것은 '옳을 가능성이 높은 것으로 판단'한다는 것이다.

귀무가설이 기각될 때 채택하는 가설로 '대립가설(Alternative hypothesis)'이라는 것이 있다. 이름 alternative에서 알 수 있듯이 단순히 귀무가설이 기각되면 채택하는 가설이다. 기호로는 보통 $\mathcal{H_{1}}$로 표현한다.

예를 들어 귀무가설이 '이 모집단의 평균이 100입니다!'라고 했을 때 대립가설은 '이 모집단의 평균은 100이 아니다.' 또는 '이 모집단의 평균은 100보다 크다.' 따위가 될 수 있다.

그렇다면 위의 상황 X에서 귀무가설과 대립가설을 정의해보면 어떻게 될까? 아래처럼 될 것이다.

귀무가설 $\mathcal{H_{0}}$: 모집단의 평균값이 $\mu'$이다.

대립가설 $\mathcal{H_{1}}$: 모집단의 평균값이 $\mu'$가 아니다.

자 그러면 어떤 방식으로 통계적 가설 검정을 하는 것일까?

먼저 이전 글에서 다룬 중심극한정리와 통계적 추정에 대한 내용이 숙지되어 있어야 한다.

A라는 사람이 모집단의 평균이 $\mu'$라고 주장하고 있다. 가장 좋은 방법은 이 모집단을 전수조사해서 평균을 내보는 것이지만 모집단이 너무 커서 시간적으로나 비용적으로나 불가능하다. 이런 상황에서는 통계적 추정에서 그랬던 것처럼 표본을 뽑아서 추론해보는 수밖에 없다.

그러니까 이사람 말대로라면 모집단의 평균이 $\mu'$라는 거니까, 중심극한정리에 의하면 표본평균의 평균 역시도 $\mu'$이어야 한다. 즉, 수학적으로 이 상황의 귀무가설과 대립가설을 수학적으로 표현해보면 아래와 같다.

귀무가설 $\mathcal{H_{0}}: E(\bar{X}) = \mu'$

대립가설 $\mathcal{H_{1}}: E(\bar{X}) \ne\mu'$

그럼 이제 표본을 뽑아보자.

아래 그림처럼 모집단에서 랜덤 샘플링한 표본의 평균을 $\bar{X_{1}}$, 분산을 $s^2$이라고 하자. 여기서는 모집단의 분산 $\sigma^2$이 알려져 있다고 가정하겠다.

중심극한정리에 의하면, 표본의 크기가 충분히 클 때(30 이상일 때) 표본평균의 분포는 다음과 같은 정규분포를 따른다고 했다. $$\bar{X}\sim\mathcal{N}(\mu, \frac{\sigma^2}{\sqrt{n}})$$

그러니까 지금처럼 표본을 하나 뽑는 행위는 아래 그림처럼 정규분포에서 표본평균을 하나 뽑는 것과 같다고 지난 글에서도 이야기했었다. 

다시 말해, 만약 A의 가설이 옳아 모집단의 평균이 $\mu'$가 맞다면 $\mu'$를 평균으로 하는 정규분포에서 샘플링을 하는 것이기 때문에, 높은 확률로 $\mu'$근처의 표본 평균이 샘플링될 것이고, 낮은 확률로 양 끝에 있는 표본평균이 샘플링될 것이다.

따라서 만약 추출한 표본의 평균 $\bar{X_{1}}$가 위 그림처럼 오른쪽 끝에 있는 놈이라면, 그 상황은 다음 두 가지로 생각해볼 수 있다.

1) A의 가설이 옳고, 낮은 확률로 $\bar{X_{1}}$가 뽑힌 것이다.

2) $\bar{X_{1}}$가 뽑힐 확률이 너무 낮으니까, A의 가설이 틀렸다고 봐야 한다. 즉, 저런 정규분포가 아닐 것이다.

'낮은 확률'의 기준을 정하는 것은 사용자의 몫이다. A의 가설이 옳다고 했을 때 $\bar{X_{1}}$가 뽑힐 확률이 1% 미만이면 A의 가설이 틀렸다고 할 수도 있고 1%가 아니라 5%, 10% 정하기 나름이다. 보통은 5%를 많이 쓰는 것 같다. 이 때의 '낮은 확률'을 '유의 수준 $\alpha$(Significant level)'라고 하며 이것을 5%로 정했다고 했을 때 $\alpha = 0.05$가 된다. 5% 미만의 확률로 뽑히는 영역 즉 $\alpha = 0.05$인 부분이 아래 그림과 같다고 했을 때, 저 영역을 $\alpha=0.05$에 해당하는 '기각역'이라고 한다. 저기서 표본평균이 뽑힌다면 귀무가설이 틀렸다고 기각할거니깐.

우리가 뽑은 표본의 평균 $\bar{X}$가 기각역 안에 있다고 해보자. 즉 사용자가 기각하기로 한 유의수준보다 낮은 확률로 뽑히는 곳에 있다(보라색 영역). 이 영역의 확률을 '유의 확률(Significant probability)' 또는 'p-value'라고 한다. 만약 보라색 영역의 확률이 2%라면 p-value=0.02가 된다.

p-value를 이용해서 귀무가설이 기각될 조건을 다시 한 번 써보면 p-value < $\frac{\alpha}{2}$라고 할 수 있다(2로 나눠주는 이유는 기각역이 양쪽 끝에 있으므로).

위 정규분포에서 p-value 즉 $\bar{X_{1}}$가 뽑힐 확률을 계산하는 것은 간단하다. 표준화를 해서 표준정규분포표를 이용하면 된다. 참고로 이런 식으로 표본 하나와 표준정규분포를 이용해 검정하는 방법을 '1표본 Z검정'이라고 한다고 한다.  

통계적 추론이란 무엇이고 어떻게 하는 것일까?
통계적 추론에는 '추정(Estimation)'과 '가설 검정(Hypothesis test)'가 있다고 한다.
이 글에서는 우선 추정에 대해서 정리한다.

다음과 같은 상황을 상상해보자.
어떤 모집단이 있다고 할 때 이 모집단의 정체를 알고 싶다. 즉, 모집단의 통계값들을 알고 싶다.
하지만 이 모집단이 너무너무 커서 모든 원소들을 하나하나 다 조사하기에는 시간도 오래 걸리고 비용도 많이 든다.
따라서 이 모집단에서 추출한 표본들만으로 모집단의 통계값들을 추정하고 싶다.
하지만 표본들은 모집단의 일부분에 불과하기 때문에 표본들로 모집단의 통계값을 추정하더라도 오차가 수반되는 것이 당연하다. 그래서 표본을 이용하여 모집단의 통계값을 추정할 때는 하나의 값으로 '점 추정(point estimation)'하기보다는 '신뢰 구간(Confidence interval)'이라고 하는 것을 이용해 '구간 추정(interval estimation)'하는 것이 대부분이다.

점 추정의 예를 들어보자.
전 세계 사람들의 평균 하루 동안의 스마트폰 사용 시간을 알고 싶다. 이 때의 모집단은 70억 명 전 세계 사람들인데 전부 다 조사하는 것은 현실적으로 불가능하다. 따라서 임의로 표본을 추출해 표본을 기반으로 모집단의 통계값을 추정하는 것이 하나의 방법이다. 예를 들어 랜덤하게 1천 명의 사람을 뽑아서, 이 집단의 평균 하루 스마트폰 사용 시간이 2.5시간이 나왔다면, 전 세계 사람들의 평균 사용 시간도 이와 같다고 추정하는 것이다. 하지만 표본의 크기가 모집단에 비해 너무 작으므로, 이 값을 신뢰하기는 어려울 것 같다. 이러한 불확실성을 보완하기 위해 구간 추정을 하게 되는 것이다.

구간으로 추정한다는 것은 말 그대로 추정하고자 하는 모집단의 평균값이 '적어도 이 구간 안에는 있어요'라고 말하는 것이다. 하지만 이것조차도 불확실성이 있으니, '적어도 이 구간 안에는 있고, $x$%만큼 신뢰할 수 있어요.'라고 보통은 표현한다. 이 때 $x$를 '신뢰도 또는 신뢰 수준(Confidence level)'이라고 한다.

그러면 어떻게 해야 이 구간이라고 하는 것을 어떻게 나타내면 좋을까?
생각해보면 점 추정에서 나온 값을 발전시킬 수 있으면 좋을 것 같다. 예를 들어, 점 추정으로 뽑은 표본의 평균이 $\bar{X}$라고 하면 '적어도 $(\bar{X} -\delta, \bar{X} +\delta)$ 안에는 모평균이 있고, 95%정도 신뢰할 수 있어요.'와 같은 식으로 말할 수 있으면 좋을 것 같다.

여기서 잠시 이전 글에서 다룬 중심극한정리를 상기시켜보자.
중심극한정리에 의하면 분포를 알 수 없는 모집단의 평균이 $\mu$, 표준편차가 $\sigma$라고 할 때, 크기 $n(\ge 30)$의 표본들을 복원추출하면 표본평균의 분포는 정규분포를 따른다는 것을 알 수 있었다. 여기서 한가지 짚고 넘어가야할 점은, 이전 글에서 중심극한정리를 다룰 때 모집단의 분산은 알고 있다는 가정했다는 것이다. 즉, $\sigma$는 여기서 알고 있는 값이다. 어쨌든 그러면 표본평균 $\bar{X}$은 아래와 같은 정규분포를 따르게 된다. $$\bar{X}\sim\mathcal{N}\left( \mu, \frac{\sigma^2}{\sqrt{n}} \right)$$

결국 표본평균은 하나의 확률변수이고 모집단에서 표본을 뽑아 표본평균을 내는 것 자체가 위 정규분포에서 표본평균 하나를 샘플링 하는 것과 같다고 볼 수 있다.

다시 '적어도 $(\bar{X} -\delta, \bar{X} +\delta$) 안에는 모평균이 있고, 95%정도 신뢰할 수 있어요.'라고 하고 싶은 상황에으로 되돌아 가보자.
아래 그림처럼 평균을 기준으로 $P\left( \mu-\delta\le\bar{X}\le\mu+\delta \right) = 0.95$가 되는 구간이 빨간색 점선 사이라고 해보자. 그리고 표본평균을 샘플링 할 때마다 각 샘플 $\bar{X}_k\pm\delta$를 신뢰구간이라고 한다면, 아래 그림처럼 빨간색 점선 사이 안에서 샘플링되는 샘플($X_1$)은 구간 안에 모평균을 반드시 포함할 것이고, 점선 바깥에서 샘플링 되는 샘플($X_2$)는 모평균을 포함시키지 못할 것이다.

다시 말해 $P\left( \mu-\delta\le\bar{X}\le\mu+\delta \right) = 0.95$이므로 빨간색 점선 사이로 표본평균이 샘플링될 확률이 95%이고 그 샘플들은 구간 안에 모평균을 포함한다. 빨간색 점선 밖으로 표본평균이 샘플링될 확률은 5%이고 그 샘플들은 모평균을 구간 안에 포함시키지 않는다. 즉, 표본평균을 샘플링해서 신뢰구간을 만들면 100개 중 95개는 모평균을 포함하므로, 95% 신뢰할 수 있다고 말할 수 있는 것이다.
그렇다면 남은 문제는 $P\left( \mu-\delta\le\bar{X}\le\mu+\delta \right) = 0.95$가 되는 $\delta$를 어떻게 구할 것인가이다. 이를 위해 다음과 같이 표준화를 한 번 해준다.

표준화를 하면 $P\left( \mu-\delta\le\bar{X}\le\mu+\delta \right) = 0.95$는 $P\left( -\delta'\le Z\le\delta' \right) = 0.95$가 되고 표준정규분포표에 의해 $\delta'$를 구하면 1.96이 나온다. 물론 이것은 신뢰수준을 95%로 했을 때의 값이고, 신뢰수준에 따라 $\delta'$값은 다르게 나온다. 주로 90%, 95%, 99%를 많이 이용한다.

여기서 잠깐! 신뢰수준이 높다는 것은 그만큼 신뢰구간이 모평균을 포함할 확률이 높다는 것이다. 모평균을 포함할 확률이 높으러면 신뢰구간이 그만큼 넓어야 한다는 것을 의미한다. 하지만 신뢰구간이 넓으면 그만큼 유용성이 떨어지게 된다. 예를 들어 '표본을 뽑아 계산해보니 전 세계 사람들의 하루 평균 스마트폰 이용 시간(모평균)은 (0, 24)시간 구간에 100%로 포함돼있어!'라고 했다고 치자. 당연히 (0, 24)구간은 모든 시간을 포함하니까 모평균이 포함될 것이다. 하지만 이렇게 추정하는 것이 무슨 의미가 있다는 것인가? 이런 trade-off 관계를 적절히 조절해서 보통은 신뢰수준 95%를 가장 흔하게 이용하는 것 같다.

결국, 통계적 추정을 할 때 통계조사를 하는 사람이 몇%의 신뢰 수준으로 추정을 하고 싶은지를 결정하면, $\delta'$값은 그에 따라 결정이 된다. 그 뒤 부등식 $-\delta'\le Z\le\delta'\Rightarrow -\delta'\le\frac{\bar{X}-\mu}{\sigma\over\sqrt{n}}\le\delta'$을 모평균 $\mu$에 대해서 풀어주면 아래와 같다. $$-\delta'\le\frac{\bar{X}-\mu}{\sigma\over\sqrt{n}}\le\delta'$$ $$\Rightarrow -\delta'\frac{\sigma}{\sqrt{n}}\le\bar{X}-\mu\le\delta'\frac{\sigma}{\sqrt{n}}$$ $$\Rightarrow -\bar{X} -\delta'\frac{\sigma}{\sqrt{n}}\le -\mu\le -\bar{X} +\delta'\frac{\sigma}{\sqrt{n}}$$ $$\Rightarrow\bar{X} -\delta'\frac{\sigma}{\sqrt{n}}\le\mu\le\bar{X} +\delta'\frac{\sigma}{\sqrt{n}}$$
이렇게 되고 여기서 신뢰구간을 $(\bar{X} -\delta'\frac{\sigma}{\sqrt{n}}, \bar{X} +\delta'\frac{\sigma}{\sqrt{n}})$로 표현한다.

그런데! 찝찝하게 남겨진 의문 하나가 떠오른다. 여기서는 표본의 크기가 30보다 크고 모분산을 알고 있다는 것을 전제로 하여, 중심극한정리에 의해 표본평균의 분포가 정규분포를 따른다고 하였다. 표본의 크기가 30보다 큰 것은 중심극한정리를 사용해야 하니깐 당연하다고 보면 된다. 그러나 모분산을 모르면 어떻게 할 것인가? 더군다나 모분산은 모르는 경우가 대다수일텐데 말이다.
이러한 문제와 관련한 상황을 다음과 같이 정리해 볼 수 있다.
1) 모분산을 알고 $n\ge 30$인 경우 $\Rightarrow$ 정규분포 $\mathcal{N}(\mu, \frac{\sigma^2}{\sqrt{n}})$ 활용.
2) 모분산을 모르고 $n\le 30$인 경우 $\Rightarrow$ t-분포 활용. 단, 모집단이 정규분포를 따라야 함.

t-분포에 대해서는 귀찮으므로 다음에!


참고한 곳
https://bskyvision.com/489#comment7834436

 통계학에서 중요하게 다뤄지는 중심극한정리의 개념에 대해 간단하게 정리하고자 한다. 나는 수학을 못하기 때문에 해봤자 와 닿지도 않는 수학적 증명과 수식은 제끼기로 했다. 위대하신 수학자님들이 잘 해놓으셨다고 하니 그냥 믿기로 하고, 실험을 통해 몸으로 느껴보기로 한다. 여러 자료를 읽어본 결과 중심극한 정리는 한 마디로 다음과 같이 정리할 수 있을 것 같다.

"모집단에서 크기 30 이상의 표본들을 복원추출하면, 모집단의 분포와 상관없이 이 표본들의 평균의 분포가 근사적으로 정규분포를 이루며, 이 때의 평균은 모집단의 평균과 같고 분산은 모집단의 분산을 표본의 크기로 나눈 것과 같다."

 여기서 왜 하필 30인지는 모르겠는데, 구글에서 검색해보면 그냥 통계학계에서의 관행이라는 것 같다.

 실제로 이 사실이 맞는지 확인하기 위해, 다음과 같이 간단한 실험을 한다.

1) 모집단의 분포를 정한다.

2) 모집단에서 크기 30의 표본을 복원추출한다.

3) 추출된 표본들의 평균의 분포가 정규분포와 가까운지 본다.

 모집단의 확률 분포는 Uniform, Norm, Gamma, Exponential, Poisson, Binom, Bernoulli로 해보기로 했다. 확률분포들은 이 링크를 참고하여 만들었다. 돌려본 결과는 아래와 같다. 왼쪽 그림은 해당 확률 분포의 확률밀도(질량)함수이고, 오른쪽이 표본평균의 분포이다.

 오른쪽 그림들에서 표본평균의 분포를 보면 정규분포와 비슷하게 보인다. 표본의 개수를 늘리면 점점 더 정규분포와 가까워진다. 

 그럼 이제 직관적인 이해를 한 번 해보자. 어떤 모집단이 있을 때, 그 모집단은 어떤 평균치를 가지고 있을 것이다. 이 모집단에서 랜덤하게 표본을 하나 샘플링하면, 이 표본의 분포는 모집단에서 어떤 원소들이 선택되느냐에 따라서 모집단과 비슷할 수도 있고, 아닐 수도 있다. 그리고 분포가 비슷하면 평균도 비슷할 것이고, 안 비슷하면 평균도 안 비슷할것이다. 그러나 아무래도 모집단의 분포를 고려하면 뽑힐 확률이 큰, 그러니까 다르게 표현하면 확률밀도(질량)함수의 함숫값이 큰 원소들이 더 많이 뽑힐 것이고, 그런 원소들의 평균은 모집단의 평균과 가까울 가능성이 클 것 같다. 따라서 복원추출을 하면, 모집단의 평균과 가까운 평균을 갖는 표본들이 많이 뽑힐 것이고 따라서 표본평균의 분포가 정규분포를 따르는 것이 자연스러워 보인다.

 그런데 모집단의 평균과 표본평균의 평균이 같아지는 것은 직관적으로 쉽게 이해가 되는데, 표본분산은 모분산을 표본의 크기로 나누어주는 것은 어떻게 이해해야 할까. 분산, 또는 표준편차는 평균으로부터 얼마나 퍼져 있는지를 나타낸다. 표본분산 = 모분산/표본의 크기 라는 것은 일단 표본분산이 모분산보다는 작다는 것이고 즉, 평균에 더 몰려있다는 뜻이고 이러한 경향은 표본의 크기가 클 수록 커진다는 것이다. 왜 그럴까? 한 번 상상을 해보자. 일단 모집단이 정규분포를 따르고 표본의 크기가 1인 경우를 가정해보자. 표본의 크기가 1이기 때문에 표본평균은 그냥 그 원소의 값이 될 것이고 그러면 표본평균의 분산이 결국 모집단에서 뽑은 원소들의 분산이 될 것이니까, 표본의 개수가 커질수록 표본평균의 분산은 모집단의 분산과 같아질 것임을 알 수 있다. 여기서 표본의 크기를 1에서 더 늘려본다고 상상해보자. 한 가지 기억할 사실은 정규분포에서 표본을 추출해서 그 원소들을 살펴보면, 모집단의 평균과 가까운 원소들이 평균과 먼 원소들보다 많을 것이라는 것이다. 따라서 표본의 크기를 늘려 한 번에 여러 개의 원소를 추출해서 평균을 내면, 평균에서 머~얼리 떨어진 원소보다는 평균에 가깝게 될 것이다. 그렇기 때문에 표본평균의 분포는 모집단보다 더 평균에 밀집된 형태를 가질 것이고, 따라서 분산이 더 작아질 수 밖에 없는 것이다.

 이와 같은 맥락에서 또 한 가지 생각해 볼 것은, 표본의 크기가 커질수록 표본의 평균의 모집단의 평균과 같을 확률이 높아진다는 것이다. 즉, 모집단에서 어떤 표본을 뽑아서 평균을 구했을 때, 표본의 크기가 크면 클수록 모집단의 평균과 가까울 것이라는 것이 자연스레 이해가 된다. 모집단에서 표본을 뽑아 평균을 구하는 행위를 표본평균을 하나 샘플링하는 것과 같다고 보는 관점에서, 표본의 크기가 클수록 평균 근처의 값이 더 많이 샘플링되니까 표본평균의 분포의 분산이 더 작아지는 것이다.

 직관적으로는 이렇고, 수학적인 증명과정은 여기와 여기서 찾아볼 수 있다.

 여기까지 중심극한정리가 어떤 것인지 알아보았다. 그런데 아직 남은 의문. 이게 왜 그렇게 중요한 걸까? 이건 귀찮으니 다음에 알아보도록 한다.