블로그

 이번에는 t분포에 대해 정리하려고 한다.

 t분포는 연속확률분포의 하나로써, 정규분포인 모집단의 평균을 추정해야 하지만 표본의 크기가 작고 모집단의 분산을 알 수 없는 경우에 이용된다고 한다.

 t분포는 Student's t-distribution이라고 불리기도 하는데, 그 이유는 처음 t분포를 발견한 William Sealy Gosset이 논문을 발표할 때 Student라는 가명을 사용했기 때문이다. 왜 그랬냐하면 그가 다니던 맥주회사 기네스에서 그가 본명으로 발표하는 것을 원치 않았는데, 자신들이 t분포를 사용한다는 것을 경쟁사한테 알리고 싶지 않았던 것이다.

1. 정의

 $Z$는 표준정규분표 $\mathcal{N}(0, 1)$를 따르는 확률변수, $Q$는 자유도 $k$인 카이제곱분포를 따르는 확률변수이고 둘이 독립일 때, 다음과 같이 정의되는 확률변수 $T$는 자유도가 $k$인 t분포를 따른다. 왜 이렇게 정의되었는지는 차차 생각해보기로 하자.

$$ T = \frac{Z}{\sqrt{\frac{Q}{k}}} \Rightarrow T \sim t_k$$

 그리고 이 확률변수는 아래와 같은 확률밀도함수를 갖는다.

$$ f(t) = \frac{\Gamma[\frac{(k+1)}{2}]}{\sqrt{\pi k} \Gamma(\frac{k}{2})}\cdot\frac{1}{[\frac{t^2}{k} + 1]^{\frac{(k+1)}{2}}}, \quad -\infty < t < \infty $$

 증명은 가볍게 넘어가고(^^), 확률밀도함수의 그래프가 어떻게 생겼는지 보자.

2. 그래프

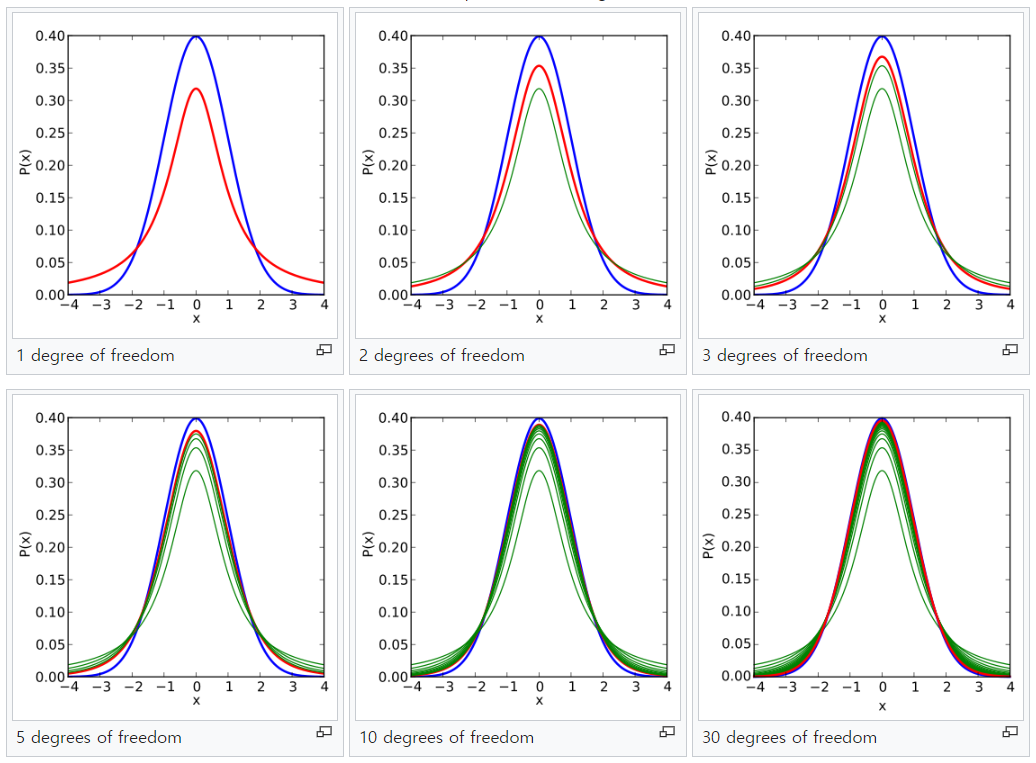
 왼쪽 위의 그림부터 보면, 파란색이 정규분포곡선($\mathcal{N}(0, 1)$)을 나타낸 것이고 빨간색이 자유도가 1인 t분포의 곡선을 나타낸 것이다. 두 곡선의 모양을 비교해보면 t분포는 정규본포와 비슷하게 종 모양이지만 양쪽 꼬리가 더 두껍고, 봉우리는 더 낮은 것을 볼 수 있다. 그리고 자유도가 커질수록 점점 정규분포와 가까워지며 자유도가 30(맨 오른쪽 아래)인 그림을 보면 거의 똑같아지는 것을 볼 수 있다. 그래서 여기서 자유도를 nomality parameter라고 부르기도 한다. 사실 이 부분에서 자유도가 커지면 왜 정규분포와 가까워지는지, 이게 t분포의 본질과 어떤 관련이 있는지 더 탐구해보고 싶지만.. 요즘 시간이 없어서 타협모드이므로.. 아쉽지만 넘어가기로 한다.

3. 표본분산과의 관계

 처음에 t분포를 모집단이 정규분포이고, 모평균을 추정하고 싶은데 모분산을 알 수 없고 표본의 크기가 작은 경우에 활용할 수 있다고 했다. 상황을 한 번 상상해보자.

• 어떤 모집단이 있고, 이 모집단은 정규분포를 따르는 것 같다.
• 이 모집단의 모평균을 추정하고 싶은데, 모분산을 몰라서 Z 통계량을 이용한 통계적 추정 방법을 없다.
• 게다가 표본의 크기 $n$이 30보다 작아서 중심극한정리에 의해 표본평균의 분포가 정규분포라고 할 수도 없을 것 같다.

 이 상황에서 어쨌든 우리는 표본을 뽑을 수 있고, 보통은 중심극한정리와 Z 통계량을 이용해서 추정을 하였지만, 이번에는 그럴 수 없는 상황이다. 그러면 우리가 알고 있는 것은 뭔가? 우리는 표본분산 $s^2$은 알 수가 있다. 따라서 Z통계량을 아래와 같이 수정해보자.

$$ \frac{\bar{X} - \mu}{\frac{\sigma}{\sqrt{n}}} \Rightarrow \frac{\bar{X} - \mu}{\frac{s}{\sqrt{n}}} $$

 단순히 모분산을 알 수가 없으니 표본분산을 이용해서 통계량을 바꿔본 것이다. 그런데 이 바뀐 통계량을 $\sigma$로 나누어주면 다음과 같은 것을 발견할 수 있다.

$$ \frac{\frac{\bar{X} - \mu}{\sigma}}{\frac{s}{\sqrt{n}\sigma}} = \frac{\frac{\bar{X} - \mu}{\frac{\sigma}{\sqrt{n}}}}{\sqrt{\frac{s^2}{\sigma^2}}}$$

$$ \Rightarrow \frac{\bar{X} - \mu}{\frac{\sigma}{\sqrt{n}}} \sim \mathcal{N}(0, 1), \quad \frac{s^2}{\sigma^2} \sim \frac{\chi_{n-1}^2}{n-1}$$

 즉, 처음에 정의한 t분포를 따르는 확률변수의 모양 $T = \frac{Z}{\sqrt{\frac{Q}{k}}}$와 같은 형태이므로, 통계량 $\frac{\bar{X} - \mu}{\frac{s}{\sqrt{n}}}$는 자유도가 $n-1$인 t분포를 따른다. 이 통계량을 t통계량이라고 하는데, 우리는 이것을 가지고 위와 같은 상황에서 통계적 추정이나 가설검정을 해 볼 수가 있게 된다. 

지난 글에서는 가설검정 중에서 1표본 Z검정에 대해서 정리하였다.

즉, 하나의 모집단과 표본에 대한 가설검정만 다루었다.

이번에는 두 모집단과 표본에 대해서 가설검정 하는 내용을 다루려고 한다(2표본 Z검정).

이 글은 훌륭한 유튜브 강의 영상인 손으로만 푸는 통계 내용을 많이 참조하였음을 밝힌다.

이번에는 어떤 두 모집단 A, B가 있다고 하자. 이때 각 모집단의 모분산 $\sigma_{A}^2$와 $\sigma_{B}^2$는 알려져있다고 가정한다.

그런데 누군가가 모집단 A의 평균 $\mu_{A}$와 모집단 B의 평균 $\mu_{B}$가 같다고 하는 의심스러운 주장을 하고 있다. 이런 의심스러운 주장(가설)을 통계적으로 검정해보려고 한다. 다르게 말하면 우리는 $\mu_{A} = \mu_{B}$임을 주장하고 싶다. 그럼 여기서 귀무가설과 대립가설은 어떻게 될까? 아래와 같이 된다.

귀무가설 $\mathcal{H_{0}}$: $\mu_{A} = \mu_{B}$

대립가설 $\mathcal{H_{1}}$: $\mu_{B} \ne \mu_{B}$  

가설 검정의 기본적인 원리는 1표본 Z검정 때와 같다. 모집단 전체를 조사하기 어려우니까 각각 표본을 뽑아 조사하도록 하고, 아래와 같이 표본을 뽑는다. 이번에도 모집단 A와 B의 모분산이 알려져 있고, 표본의 크기 $n_A$와 $n_B$는 30보다 크다고 가정한다.

표본의 크기가 30보다 크므로, 중심극한 정리에 의해, 다음이 성립한다.

$$\bar{X_{A}}\sim\mathcal{N}(\mu_{A}, \frac{\sigma_{A}^2}{n_{A}}),$$ $$\bar{X_{B}}\sim\mathcal{N}(\mu_{B}, \frac{\sigma_{B}^2}{n_{B}})$$

이전에 1표본 Z검정에서는 모집단의 평균이 특정 값인지 아닌지를 따지는 것이어서 $E(\bar{X})$를 특정 값 $\mu'$인 정규분포로 놓고 표준정규분포를 이용해 p-value를 구하고 유의수준 $\alpha$와 비교했다. 근데 여기서는 귀무가설 자체가 어떤 특정 값과 비교하는 것이 아니고, 값을 모르는 두 모집단의 평균이 같다라는 것이기 때문에 이전과 같이 할 수가 없다. 그래서 약간의 기술을 사용하는데, 다음과 같이 변수를 새로 정의한다. $$Y = \bar{X}_{A} - \bar{X}_{B}$$

이렇게 해주는 이유는 어차피 $\mu_{A}$와 $\mu_{B}$를 알 수 없으니, 둘의 차이를 새로운 관점으로 해서 접근해보겠다는 것이다.

그러면 귀무가설은 $$\mu_{A} = \mu_{B}$$ $$\Leftrightarrow E(Y) = \mu_{A} - \mu_{B} = 0$$

이 된다. 그런데 $\bar{X}_{A}$와 $\bar{X}_{B}$가 각각 정규분포를 따르므로, $Y$는 다음과 같은 정규분포를 따른다. $Y$가 아래와 같은 정규분포를 따른다는 것은 수학적 증명이 필요한데, 자세한 증명은 손으로만 푸는 통계 채널을 참고하도록 하고 여기서는 생략한다. $$Y\sim\mathcal{N}(0, \frac{\sigma_{A}^2}{n_{A}} + \frac{\sigma_{B}^2}{n_{B}})$$

모집단 A, B에서 각각 뽑은 표본의 평균을 $\bar{X_{A, 1}}, \bar{X_{B, 1}}$이라고 하면 $Y_{1} = \bar{X}_{A, 1} - \bar{X}_{B, 1}$이다. 즉, 모집단 A, B에서 표본을 하나씩 뽑으면 위 정규분포에서도 $Y$에 대한 표본을 하나 뽑은 것과 같다. 유의수준 $\alpha$를 0.05로 정했다고 하고, 어쨌든 이 상태에서 $Y$의 분포에 대한 평균과 분산을 알고 있으니 표준정규분포를 이용해서 $Y_{1}$에 대한 p-value를 구할 수가 있다. 만약 구한 p-value가 $\alpha$보다 작으면, 즉 표본이 기각역 안에 있으면 귀무가설을 기각하고 대립가설을 채택할 수가 있게 된다.

다시 말해서, 두 모집단 A, B의 평균의 차이가 0이다 라는 귀무가설이 참이라고 했을 때, 표본을 추출해봤더니 뽑힐 확률이 5%미만인 표본이 나왔다면, 귀무가설이 잘못되었다고 볼 수 있는 것이다.