블로그

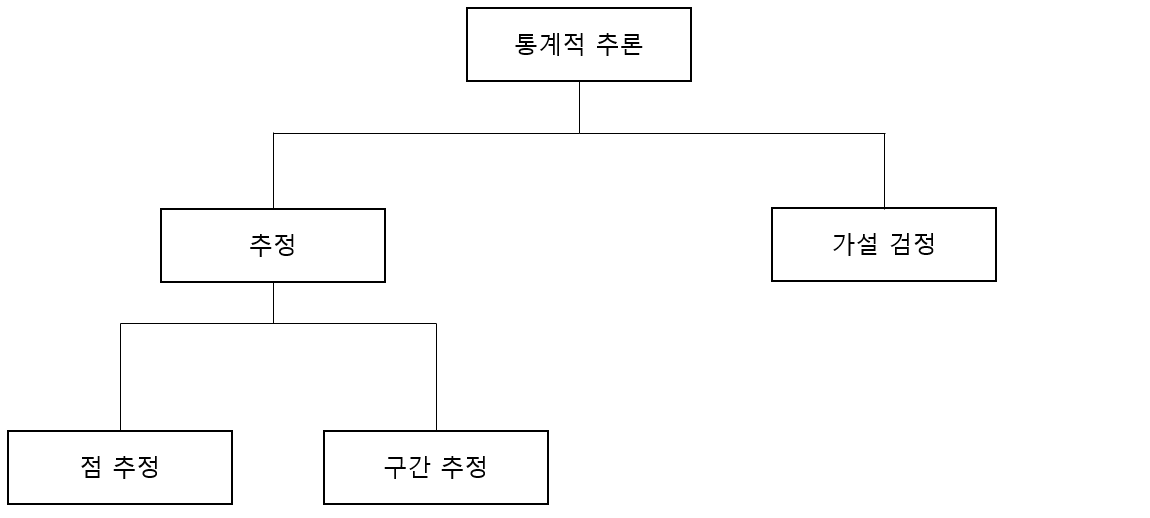
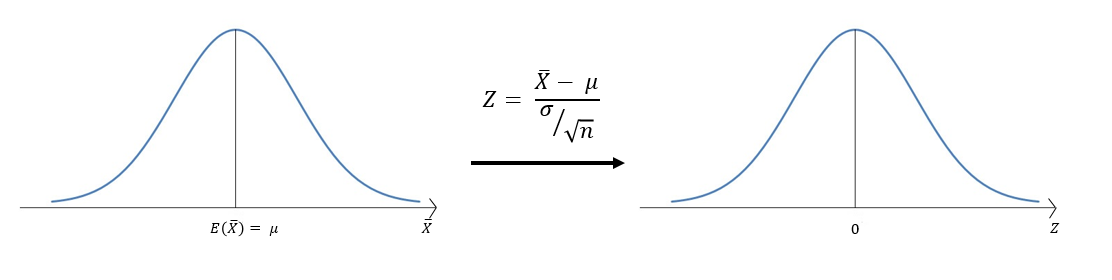이번엔 가설 검정에 대해 정리하려고 한다.

정리하려고 여러 자료를 찾아보던 중 엄청나게 설명을 잘 해놓은 유튜브 영상이 있어, 이 영상에 나온 내용 위주로 정리하려고 한다. 정말이지 너무 설명을 깔끔하게 잘 해놔서 존경스럽다. 나도 이렇게 명확하고 깔끔하게 잘 설명할 수 있으면 좋으련만. 영상 주소는 여기. 나처럼 통계를 공부해보려는 사람에게 아주 유용한 강의가 채널에 잔뜩 올라와있다. 강추!!

그럼 가설 검정에 대한 이야기를 시작해보자.

가설 검정이란, 말그대로 어떤 '가설'이 있을 때, 그 가설이 맞는지 틀린지 통계적인 관점에서 '검정'해보는 것이다.

먼저 어떤 상황에서 가설 검정을 하게 되는지를 보면 좀 더 순조롭게 이해가 된다.

상황 X)

어떤 분포를 알 수 없는 모집단이 있을 때, 어떤 사람 A가 와서 이 모집단의 평균값이 $\mu'$라고 밑도 끝도 없는 주장을 해대고 있다. 나는 대충 어림잡아 봐도 $\mu'$은 아닐 것 같아 상당의 의심이 드는데, 이 사람이 사기꾼인지 아닌지 알아보기 위해 통계적인 방법으로 A의 '가설'을 검증해보려고 한다.

여기서 A의 주장을 즉 가설을 '귀무가설(Null hypothesis)'이라고 한다.

그 이름도 어려운 귀무가설은 돌아갈 귀, 없을 무를 써서 무無로 돌아갈 가설을 의미한다. 즉, 터무니 없는 가설이므로 기각될 가설이라는 뜻이다. 기호로는 보통 $\mathcal{H_{0}}$로 표현한다.

아무리 터무니없어 보여도 귀무가설이 참이 확률이 있다. 따라서 귀무가설은 기각될 수도 있고 채택될 수도 있다. 쉽게 말해 통계적으로 검정을 해보았을 때 기각된다 함은 '옳지 않은 가능성이 높다고 판단'한다는 것이고 채택된다는 것은 '옳을 가능성이 높은 것으로 판단'한다는 것이다.

귀무가설이 기각될 때 채택하는 가설로 '대립가설(Alternative hypothesis)'이라는 것이 있다. 이름 alternative에서 알 수 있듯이 단순히 귀무가설이 기각되면 채택하는 가설이다. 기호로는 보통 $\mathcal{H_{1}}$로 표현한다.

예를 들어 귀무가설이 '이 모집단의 평균이 100입니다!'라고 했을 때 대립가설은 '이 모집단의 평균은 100이 아니다.' 또는 '이 모집단의 평균은 100보다 크다.' 따위가 될 수 있다.

그렇다면 위의 상황 X에서 귀무가설과 대립가설을 정의해보면 어떻게 될까? 아래처럼 될 것이다.

귀무가설 $\mathcal{H_{0}}$: 모집단의 평균값이 $\mu'$이다.

대립가설 $\mathcal{H_{1}}$: 모집단의 평균값이 $\mu'$가 아니다.

자 그러면 어떤 방식으로 통계적 가설 검정을 하는 것일까?

먼저 이전 글에서 다룬 중심극한정리와 통계적 추정에 대한 내용이 숙지되어 있어야 한다.

A라는 사람이 모집단의 평균이 $\mu'$라고 주장하고 있다. 가장 좋은 방법은 이 모집단을 전수조사해서 평균을 내보는 것이지만 모집단이 너무 커서 시간적으로나 비용적으로나 불가능하다. 이런 상황에서는 통계적 추정에서 그랬던 것처럼 표본을 뽑아서 추론해보는 수밖에 없다.

그러니까 이사람 말대로라면 모집단의 평균이 $\mu'$라는 거니까, 중심극한정리에 의하면 표본평균의 평균 역시도 $\mu'$이어야 한다. 즉, 수학적으로 이 상황의 귀무가설과 대립가설을 수학적으로 표현해보면 아래와 같다.

귀무가설 $\mathcal{H_{0}}: E(\bar{X}) = \mu'$

대립가설 $\mathcal{H_{1}}: E(\bar{X}) \ne\mu'$

그럼 이제 표본을 뽑아보자.

아래 그림처럼 모집단에서 랜덤 샘플링한 표본의 평균을 $\bar{X_{1}}$, 분산을 $s^2$이라고 하자. 여기서는 모집단의 분산 $\sigma^2$이 알려져 있다고 가정하겠다.

중심극한정리에 의하면, 표본의 크기가 충분히 클 때(30 이상일 때) 표본평균의 분포는 다음과 같은 정규분포를 따른다고 했다. $$\bar{X}\sim\mathcal{N}(\mu, \frac{\sigma^2}{\sqrt{n}})$$

그러니까 지금처럼 표본을 하나 뽑는 행위는 아래 그림처럼 정규분포에서 표본평균을 하나 뽑는 것과 같다고 지난 글에서도 이야기했었다. 

다시 말해, 만약 A의 가설이 옳아 모집단의 평균이 $\mu'$가 맞다면 $\mu'$를 평균으로 하는 정규분포에서 샘플링을 하는 것이기 때문에, 높은 확률로 $\mu'$근처의 표본 평균이 샘플링될 것이고, 낮은 확률로 양 끝에 있는 표본평균이 샘플링될 것이다.

따라서 만약 추출한 표본의 평균 $\bar{X_{1}}$가 위 그림처럼 오른쪽 끝에 있는 놈이라면, 그 상황은 다음 두 가지로 생각해볼 수 있다.

1) A의 가설이 옳고, 낮은 확률로 $\bar{X_{1}}$가 뽑힌 것이다.

2) $\bar{X_{1}}$가 뽑힐 확률이 너무 낮으니까, A의 가설이 틀렸다고 봐야 한다. 즉, 저런 정규분포가 아닐 것이다.

'낮은 확률'의 기준을 정하는 것은 사용자의 몫이다. A의 가설이 옳다고 했을 때 $\bar{X_{1}}$가 뽑힐 확률이 1% 미만이면 A의 가설이 틀렸다고 할 수도 있고 1%가 아니라 5%, 10% 정하기 나름이다. 보통은 5%를 많이 쓰는 것 같다. 이 때의 '낮은 확률'을 '유의 수준 $\alpha$(Significant level)'라고 하며 이것을 5%로 정했다고 했을 때 $\alpha = 0.05$가 된다. 5% 미만의 확률로 뽑히는 영역 즉 $\alpha = 0.05$인 부분이 아래 그림과 같다고 했을 때, 저 영역을 $\alpha=0.05$에 해당하는 '기각역'이라고 한다. 저기서 표본평균이 뽑힌다면 귀무가설이 틀렸다고 기각할거니깐.

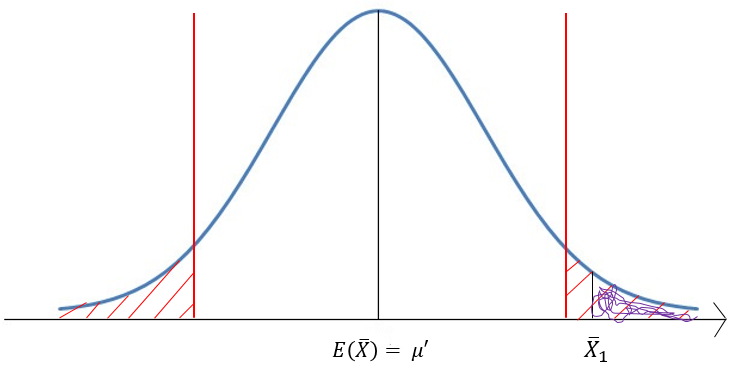
우리가 뽑은 표본의 평균 $\bar{X}$가 기각역 안에 있다고 해보자. 즉 사용자가 기각하기로 한 유의수준보다 낮은 확률로 뽑히는 곳에 있다(보라색 영역). 이 영역의 확률을 '유의 확률(Significant probability)' 또는 'p-value'라고 한다. 만약 보라색 영역의 확률이 2%라면 p-value=0.02가 된다.

p-value를 이용해서 귀무가설이 기각될 조건을 다시 한 번 써보면 p-value < $\frac{\alpha}{2}$라고 할 수 있다(2로 나눠주는 이유는 기각역이 양쪽 끝에 있으므로).

위 정규분포에서 p-value 즉 $\bar{X_{1}}$가 뽑힐 확률을 계산하는 것은 간단하다. 표준화를 해서 표준정규분포표를 이용하면 된다. 참고로 이런 식으로 표본 하나와 표준정규분포를 이용해 검정하는 방법을 '1표본 Z검정'이라고 한다고 한다.  

통계적 추론이란 무엇이고 어떻게 하는 것일까?
통계적 추론에는 '추정(Estimation)'과 '가설 검정(Hypothesis test)'가 있다고 한다.
이 글에서는 우선 추정에 대해서 정리한다.

다음과 같은 상황을 상상해보자.
어떤 모집단이 있다고 할 때 이 모집단의 정체를 알고 싶다. 즉, 모집단의 통계값들을 알고 싶다.
하지만 이 모집단이 너무너무 커서 모든 원소들을 하나하나 다 조사하기에는 시간도 오래 걸리고 비용도 많이 든다.
따라서 이 모집단에서 추출한 표본들만으로 모집단의 통계값들을 추정하고 싶다.
하지만 표본들은 모집단의 일부분에 불과하기 때문에 표본들로 모집단의 통계값을 추정하더라도 오차가 수반되는 것이 당연하다. 그래서 표본을 이용하여 모집단의 통계값을 추정할 때는 하나의 값으로 '점 추정(point estimation)'하기보다는 '신뢰 구간(Confidence interval)'이라고 하는 것을 이용해 '구간 추정(interval estimation)'하는 것이 대부분이다.

점 추정의 예를 들어보자.
전 세계 사람들의 평균 하루 동안의 스마트폰 사용 시간을 알고 싶다. 이 때의 모집단은 70억 명 전 세계 사람들인데 전부 다 조사하는 것은 현실적으로 불가능하다. 따라서 임의로 표본을 추출해 표본을 기반으로 모집단의 통계값을 추정하는 것이 하나의 방법이다. 예를 들어 랜덤하게 1천 명의 사람을 뽑아서, 이 집단의 평균 하루 스마트폰 사용 시간이 2.5시간이 나왔다면, 전 세계 사람들의 평균 사용 시간도 이와 같다고 추정하는 것이다. 하지만 표본의 크기가 모집단에 비해 너무 작으므로, 이 값을 신뢰하기는 어려울 것 같다. 이러한 불확실성을 보완하기 위해 구간 추정을 하게 되는 것이다.

구간으로 추정한다는 것은 말 그대로 추정하고자 하는 모집단의 평균값이 '적어도 이 구간 안에는 있어요'라고 말하는 것이다. 하지만 이것조차도 불확실성이 있으니, '적어도 이 구간 안에는 있고, $x$%만큼 신뢰할 수 있어요.'라고 보통은 표현한다. 이 때 $x$를 '신뢰도 또는 신뢰 수준(Confidence level)'이라고 한다.

그러면 어떻게 해야 이 구간이라고 하는 것을 어떻게 나타내면 좋을까?
생각해보면 점 추정에서 나온 값을 발전시킬 수 있으면 좋을 것 같다. 예를 들어, 점 추정으로 뽑은 표본의 평균이 $\bar{X}$라고 하면 '적어도 $(\bar{X} -\delta, \bar{X} +\delta)$ 안에는 모평균이 있고, 95%정도 신뢰할 수 있어요.'와 같은 식으로 말할 수 있으면 좋을 것 같다.

여기서 잠시 이전 글에서 다룬 중심극한정리를 상기시켜보자.
중심극한정리에 의하면 분포를 알 수 없는 모집단의 평균이 $\mu$, 표준편차가 $\sigma$라고 할 때, 크기 $n(\ge 30)$의 표본들을 복원추출하면 표본평균의 분포는 정규분포를 따른다는 것을 알 수 있었다. 여기서 한가지 짚고 넘어가야할 점은, 이전 글에서 중심극한정리를 다룰 때 모집단의 분산은 알고 있다는 가정했다는 것이다. 즉, $\sigma$는 여기서 알고 있는 값이다. 어쨌든 그러면 표본평균 $\bar{X}$은 아래와 같은 정규분포를 따르게 된다. $$\bar{X}\sim\mathcal{N}\left( \mu, \frac{\sigma^2}{\sqrt{n}} \right)$$

결국 표본평균은 하나의 확률변수이고 모집단에서 표본을 뽑아 표본평균을 내는 것 자체가 위 정규분포에서 표본평균 하나를 샘플링 하는 것과 같다고 볼 수 있다.

다시 '적어도 $(\bar{X} -\delta, \bar{X} +\delta$) 안에는 모평균이 있고, 95%정도 신뢰할 수 있어요.'라고 하고 싶은 상황에으로 되돌아 가보자.
아래 그림처럼 평균을 기준으로 $P\left( \mu-\delta\le\bar{X}\le\mu+\delta \right) = 0.95$가 되는 구간이 빨간색 점선 사이라고 해보자. 그리고 표본평균을 샘플링 할 때마다 각 샘플 $\bar{X}_k\pm\delta$를 신뢰구간이라고 한다면, 아래 그림처럼 빨간색 점선 사이 안에서 샘플링되는 샘플($X_1$)은 구간 안에 모평균을 반드시 포함할 것이고, 점선 바깥에서 샘플링 되는 샘플($X_2$)는 모평균을 포함시키지 못할 것이다.

다시 말해 $P\left( \mu-\delta\le\bar{X}\le\mu+\delta \right) = 0.95$이므로 빨간색 점선 사이로 표본평균이 샘플링될 확률이 95%이고 그 샘플들은 구간 안에 모평균을 포함한다. 빨간색 점선 밖으로 표본평균이 샘플링될 확률은 5%이고 그 샘플들은 모평균을 구간 안에 포함시키지 않는다. 즉, 표본평균을 샘플링해서 신뢰구간을 만들면 100개 중 95개는 모평균을 포함하므로, 95% 신뢰할 수 있다고 말할 수 있는 것이다.
그렇다면 남은 문제는 $P\left( \mu-\delta\le\bar{X}\le\mu+\delta \right) = 0.95$가 되는 $\delta$를 어떻게 구할 것인가이다. 이를 위해 다음과 같이 표준화를 한 번 해준다.

표준화를 하면 $P\left( \mu-\delta\le\bar{X}\le\mu+\delta \right) = 0.95$는 $P\left( -\delta'\le Z\le\delta' \right) = 0.95$가 되고 표준정규분포표에 의해 $\delta'$를 구하면 1.96이 나온다. 물론 이것은 신뢰수준을 95%로 했을 때의 값이고, 신뢰수준에 따라 $\delta'$값은 다르게 나온다. 주로 90%, 95%, 99%를 많이 이용한다.

여기서 잠깐! 신뢰수준이 높다는 것은 그만큼 신뢰구간이 모평균을 포함할 확률이 높다는 것이다. 모평균을 포함할 확률이 높으러면 신뢰구간이 그만큼 넓어야 한다는 것을 의미한다. 하지만 신뢰구간이 넓으면 그만큼 유용성이 떨어지게 된다. 예를 들어 '표본을 뽑아 계산해보니 전 세계 사람들의 하루 평균 스마트폰 이용 시간(모평균)은 (0, 24)시간 구간에 100%로 포함돼있어!'라고 했다고 치자. 당연히 (0, 24)구간은 모든 시간을 포함하니까 모평균이 포함될 것이다. 하지만 이렇게 추정하는 것이 무슨 의미가 있다는 것인가? 이런 trade-off 관계를 적절히 조절해서 보통은 신뢰수준 95%를 가장 흔하게 이용하는 것 같다.

결국, 통계적 추정을 할 때 통계조사를 하는 사람이 몇%의 신뢰 수준으로 추정을 하고 싶은지를 결정하면, $\delta'$값은 그에 따라 결정이 된다. 그 뒤 부등식 $-\delta'\le Z\le\delta'\Rightarrow -\delta'\le\frac{\bar{X}-\mu}{\sigma\over\sqrt{n}}\le\delta'$을 모평균 $\mu$에 대해서 풀어주면 아래와 같다.$$-\delta'\le\frac{\bar{X}-\mu}{\sigma\over\sqrt{n}}\le\delta'$$ $$\Rightarrow -\delta'\frac{\sigma}{\sqrt{n}}\le\bar{X}-\mu\le\delta'\frac{\sigma}{\sqrt{n}}$$ $$\Rightarrow -\bar{X} -\delta'\frac{\sigma}{\sqrt{n}}\le -\mu\le -\bar{X} +\delta'\frac{\sigma}{\sqrt{n}}$$ $$\Rightarrow\bar{X} -\delta'\frac{\sigma}{\sqrt{n}}\le\mu\le\bar{X} +\delta'\frac{\sigma}{\sqrt{n}}$$
이렇게 되고 여기서 신뢰구간을 $(\bar{X} -\delta'\frac{\sigma}{\sqrt{n}}, \bar{X} +\delta'\frac{\sigma}{\sqrt{n}})$로 표현한다.

그런데! 찝찝하게 남겨진 의문 하나가 떠오른다. 여기서는 표본의 크기가 30보다 크고 모분산을 알고 있다는 것을 전제로 하여, 중심극한정리에 의해 표본평균의 분포가 정규분포를 따른다고 하였다. 표본의 크기가 30보다 큰 것은 중심극한정리를 사용해야 하니깐 당연하다고 보면 된다. 그러나 모분산을 모르면 어떻게 할 것인가? 더군다나 모분산은 모르는 경우가 대다수일텐데 말이다.
이러한 문제와 관련한 상황을 다음과 같이 정리해 볼 수 있다.
1) 모분산을 알고 $n\ge 30$인 경우 $\Rightarrow$ 정규분포 $\mathcal{N}(\mu, \frac{\sigma^2}{\sqrt{n}})$ 활용.
2) 모분산을 모르고 $n\le 30$인 경우 $\Rightarrow$ t-분포 활용. 단, 모집단이 정규분포를 따라야 함.

t-분포에 대해서는 귀찮으므로 다음에!


참고한 곳
https://bskyvision.com/489#comment7834436